Boba Devlog #2: Compiling Arrays
2023-Sep-04
Boba is a compiler project I’m working on to learn how to implement type system, code optimization passes and code generation. It compiles a language with Rust-like syntax and C-like semantics to x86-64 assembly. In this post, I’d like to explain how it compiles arrays.
1 Syntax and Semantics of Arrays
The syntax for arrays resembles that of Rust and the semantics follow that of C.
An array is a collection of elements stored in a contiguous block of memory on the stack. It evaluates to a pointer to the first element in the array and this pointer can be assigned to other variables, passed into functions and used in subscript expressions to access any element of the array. But, returning an array (pointer) from a function will result in garbage values or segmentation fault. When an array is passed into a print statement, it will print all the elements in the array.
fn sum(array: [i32; 5]) -> i32 {
let mut total = 0;
for (let mut i = 0; i < 5; i = i + 1) {
total = total + array[i];
}
return total;
}
fn main() {
let array = [1, 2, 3, 4, 5];
let total = sum(array);
println("Sum of {} = {}", array, total); // Sum of [1, 2, 3, 4, 5] = 15
}
2 Memory Layout
To understand how arrays can be expressed in assembly, it helped me a lot to visualize the memory layout of arrays.
2.1 One-dimensional Array
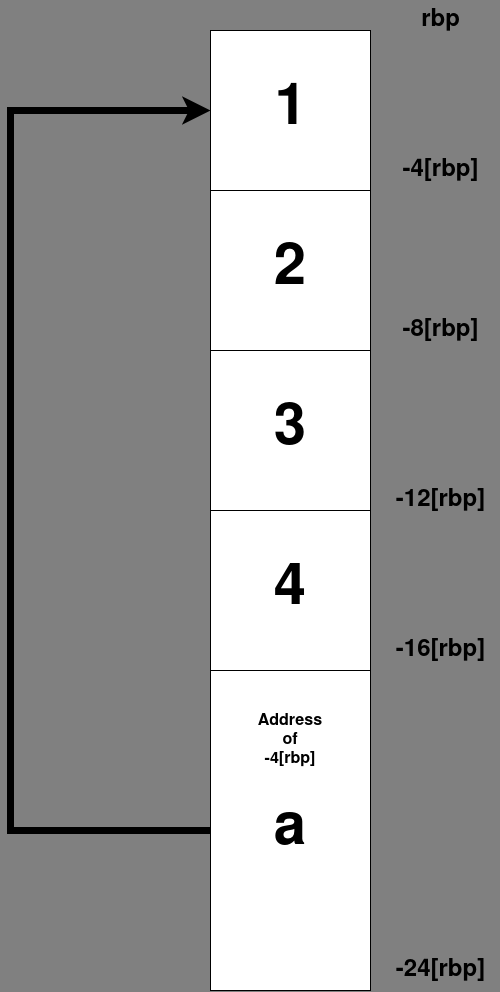
The code let a = [1, 2, 3, 4]; will have the following memory representation:
 Here,
Here, rbp is the base pointer of the current stack frame and -4[rbp] can be interpreted as four bytes below the base pointer.
Each number in the array is stored in a four byte interval between rbp and -16[rbp] and the variable a (pointer to the first element in the array) takes up the eight bytes immediately after -16[rbp]. The address of each value decreases since the stack grows downward.
2.2 Two-dimensional Array
The representation of a two-dimensional array is similar to an one-dimensional array but there is a level of indirection to take care of. For example, the code let a = [[1, 2], [3, 4]]; will be represented as:
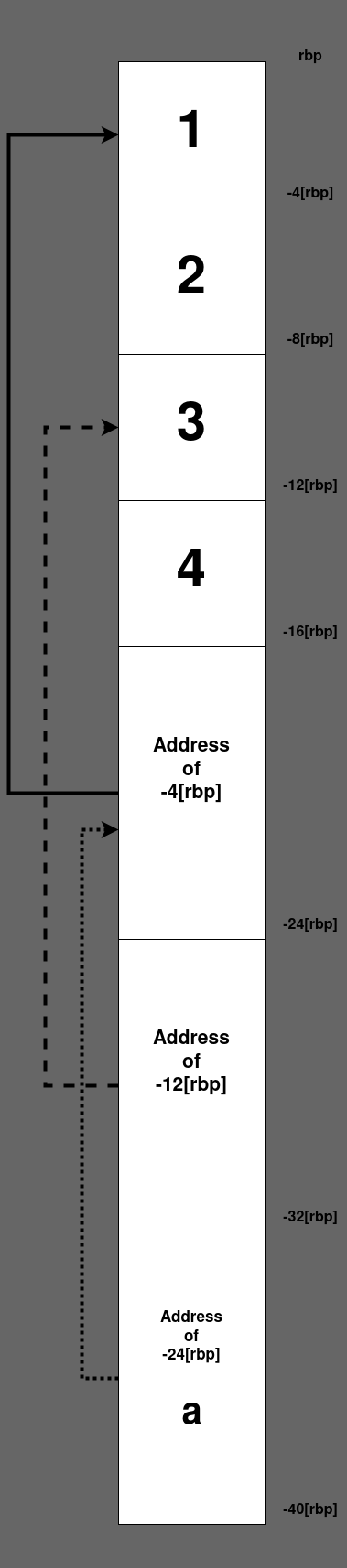 The first element in the array is a pointer to the first array and the second element is a pointer to the second array. The data is tightly packed because the addresses naturally align for the numbers (four bytes each) and pointers (eight bytes each). When the values don’t align naturally there will be some padding added in between the values.
The first element in the array is a pointer to the first array and the second element is a pointer to the second array. The data is tightly packed because the addresses naturally align for the numbers (four bytes each) and pointers (eight bytes each). When the values don’t align naturally there will be some padding added in between the values.
3 Subscript Expressions
A subscript expression numbers[i] is used to access the element at index i in array numbers. On the assembly level, this is expressed by dereferencing the pointer obtained by adding the pointer to the first element in numbers with the product of i and the size of an element in numbers.
Internally, this gets compiled to the lea instruction to obtain the offset by multiplying the index and element size, the add instruction to increment the array pointer with the offset and the indirect addressing mode to dereference the pointer.
4 Printing Arrays
An array is just a pointer but when it is passed into a print statement, the programmer, for the most part, expects all the elements in the array to be printed rather than the pointer address. Also, since the length of the array and the type of each element in the array is known at compile time, the compiler can easily access all the elements of the array given its base pointer.
For example, if an array let array = [1, 2, 3, 4]; is passed into print as:
println("{}", array);
The print statement can be transformed into:
println("[%d, %d, %d, %d]", array[0], array[1], array[2], array[3]);
A small obstruction to express the transformation in assembly is the System V ABI calling convention where the first six arguments to a function are passed in registers and the rest are pushed onto the stack in reverse order. But, for an array where the first few elements are passed in registers and the rest are pushed onto the stack, it is complicated for the compiler to evaluate the first few elements in left-to-right order and then evaluate the rest that goes onto the stack in right-to-left order1.
So, I decided to evaluate all arguments to a print statement (including an array’s elements) in right-to-left order. This allowed me to iterate over the arguments only once and place all the arguments in appropriate registers and positions on the stack.
Footnotes:
Maybe there is an efficient and elegant way to implement this but I cannot figure it out.